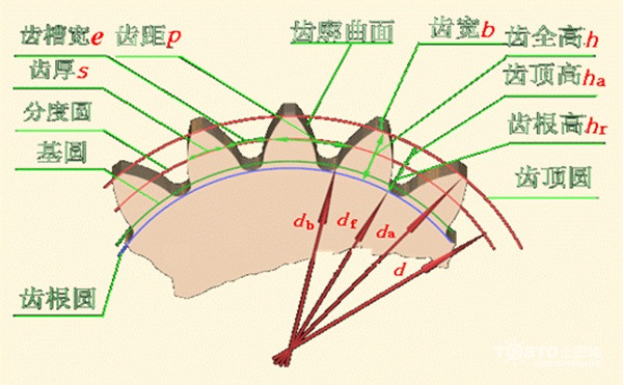
1. Te maha o ngā niho Z Te tapeke o ngā niho o tētahitaputapu
2, modulus m Ko te hua o te tawhiti niho me te maha o ngā niho he ōrite ki te porowhita o te porowhita wehewehe, arā, pz= πd,

ko z he tau tūturu, ā, ko π he tau koretake. Kia whai tikanga ai a d, ko te tikanga he tikanga tika a p/π ka kiia ko te modulus. Arā: m=p/π
3, ko te whānui o te porowhita tohu d me te rahi o te niho o te taputapu ka whakatauhia i runga i tēnei porowhita d=mz tāruatia te tuhinga katoa 24, te whānui o te porowhita o runga d. Ā, ko te whānui o te porowhita pūtake de pānui mata katoa mai i te tātai tatau o te teitei o te tihi me te teitei o te pakiaka, ka taea te whakaputa i te tātai tatau o te whānui o te porowhita tihi me te whānui o te porowhita pūtake:
d.=d+2h.=mz+2m=m(z+2)

Ko te nui ake o te modulus o te wira, ko te teitei ake, ko te matotoru ake hoki o ngā niho, mena ka nui ake te maha o ngā niho o te

taputapuHe mea tino pono, ko te nui ake o te rahi radial o te wira. Ka hangaia ngā paerewa raupapa modular kia rite ki ngā whakaritenga o te hoahoa, te hanga me te tirotiro. Mō ngā taputapu he niho kore-tika, ko te modulus he rerekētanga i waenga i te modulus noa mn, te modulus mutunga ms me te modulus axial mx, e ahu mai ana i te ōwehenga o ō rātou pitch (pitch noa, pitch mutunga me te pitch axial) ki te PI, ā, kei roto hoki i ngā mirimita. Mō ngā taputapu bevel, kei te kōwae te kōwae pito nui me, te kōwae toharite mm me te kōwae pito iti m1. Mō te taputapu, kei reira te modulus taputapu e rite ana mo me ētahi atu. He whānui te whakamahinga o ngā kōwae paerewa. I roto i te puku taputapu ine, te puku kutukutu, te puku whitiki taputapu tukutahi me te ratchet, te hononga taputapu, te spline me ētahi atu wāhanga, ko te modulus paerewa te tawhā taketake. He mahi tawhā taketake tana i roto i te hoahoa, te hanga me te tiaki i ngā wāhanga o runga ake nei.

1) Ko te modulus te tohu i te rahi o ngā niho. Ko te R-module te ōwehenga o te pikinga o te porowhita wehewehe ki te PI (π), e whakaaturia ana i roto i ngā mirimita (mm). Haunga ngā modules, kei a tātou te Diametral pitch (CP) me te DP (Diametral pitch) hei whakaahua i te rahi o ngā niho. Ko te diametral pitch te roa o te pewa wehewehe i waenganui i ngā pūwāhi ōrite i runga i ngā niho e rua e tata ana.

2) He aha te "diameter o te porowhita tohutoro"? Ko te diameter o te porowhita tohutoro ko te diameter tohutoro o tetaputapuKo ngā mea matua e rua e whakatau ana i te rahi o te taputapu ko te modulus me te maha o ngā niho, ā, ko te diameter o te porowhita wehewehe he ōrite ki te hua o te maha o ngā niho me te modulus (te mata pito).
3) He aha te "Koki Pēhanga"? Ko te koki koi i waenganui i te rārangi radial i te whakawhitinga o te āhua niho me te patō o te pūwāhi e kiia ana ko te Koki Pēhanga o te porowhita tohutoro. I te nuinga o te wā, ko te Koki Pēhanga e pā ana ki te Koki Pēhanga o te porowhita tohutoro. Ko te Koki Pēhanga e whakamahia whānuitia ana ko te 20°; heoi, ka whakamahia hoki ngā taputapu me ngā koki pēhanga o te 14.5°, 15°, 17.5°, me te 22.5°.

4) He aha te rerekētanga i waenga i te noke upoko kotahi me te noke upoko rua? Ko te maha o ngā niho porowhita o te noke e kiia ana ko te "maha o ngā upoko", he rite ki te maha o ngā niho o te taputapu. Mēnā he maha ngā upoko, ka nui ake te koki mata.

5) Me pēhea te wehewehe i te R (ringa matau)? Ko te kakau taputapu L (ringa maui) he poutū te whenua o te kakau taputapu papatahi, ko te niho e piko ana ki te taha matau ko te taputapu matau, ko te niho e piko ana ki te taha maui ko te taputapu maui.

6) He aha te rerekētanga i waenga i te M (modulus) me te CP (pitch)? Ko te CP (Circular pitch) te pitch porowhita o ngā niho i runga i te porowhita tohu. He rite te waeine ki te modulus i roto i ngā mirimita. Mā te CP wehea e te PI (π) ka puta ko te M (modulus). Ko te whanaungatanga i waenga i te M (modulus) me te CP e whakaaturia ana penei. M (modulus) =CP/π (PI) He waeine e rua mō te rahi o te niho. (Ko te porowhita wehewehe = nd=zpd=zp/ l/PI e kiia ana ko te modulus

7) He aha te "whakamuri"? Ko te āputa i waenganui i ngā mata niho o tētahi takirua taputapu ina honoa. He tawhā nui te whakamuri mō te maeneene o te mahi honohono taputapu. 8) He aha te rerekētanga i waenganui i te kaha piko me te kaha o te mata niho? I te nuinga o te wā, me whakaaro te kaha o ngā taputapu mai i ngā āhuatanga e rua: te piko me te kaha o te mata niho. Ko te kaha piko ko te kaha o te niho e tuku ana i te mana hei ātete i te pakaru o te niho i te pūtake nā te mahi a te kaha piko. Ko te kaha o te mata niho ko te kaha waku o te mata niho i te wā e pa ana ki te niho kua honoa. 9) I roto i te kaha piko me te kaha o te mata niho, he aha te kaha e whakamahia ana hei pūtake mō te whiriwhiri i te taputapu? I te nuinga o te wā, me matapakihia te piko me te kaha o te mata niho. Heoi, i te wā e whiriwhiri ana i ngā taputapu e kore e whakamahia pinepine, ngā taputapu ringaringa, me ngā taputapu honohono tere-iti, tera ētahi wā ka whiriwhiria te kaha piko anake. Hei whakamutunga, kei te kaihoahoa te whakatau.